Vorbemerkung
- Die Schüler sollen entdecken, dass die Bestandsfunktion
eine Stammfunktion der Änderungsrate ist.
- Die Graphen der Änderungsrate und der Bestandsfunktion
können die Schülerinnen und Schüler mit Hilfe einer
Tabellenkalkulation und eines Funktionenplotters gewinnen,
vergleichen und Beziehungen zwischen diesen herstellen.
- Fragen, wie die Genauigkeit der Näherung erhöht werden kann,
geben Anlass zu anschaulichen Grenzwertüberlegungen.
- Da der Rekonstruktionsprozess auch bei einer abstrakt
gegebenen Randfunktion möglich ist, wird für
Bestandsfunktionen der Fachbegriff Integralfunktion eingeführt
und der Zusammenhang zwischen Rand- und Integralfunktion im
Hauptsatz formuliert (ggf. auch im Lehrervortrag).
- In den Anwendungen steht mit dem Hauptsatz neben dem
numerischen Verfahren ein alternativer Lösungsweg zur
Berechnung von Gesamtbeständen zur Verfügung.
- Davon abgegrenzt wird die Berechnung von Flächeninhalten,
bei der auch Intervalladditivität und Linearität (bei der
Berechnung von Flächen zwischen Kurven) thematisiert werden.
Bei der Berechnung der Flächeninhalte zwischen Graphen werden
die Schnittstellen in der Regel numerisch mit dem GTR
bestimmt.
- Bei der Berechnung der Volumina wird stark auf Analogien zur
Flächenberechnung verwiesen. (Gedanklich wird mit einem
„Eierschneider“ der Rotationskörper in berechenbare Zylinder
zerlegt, analog den Rechtecken oder Trapezen bei der
Flächenberechnung. Auch die jeweiligen Summenformeln weisen
Entsprechungen auf.)
- Mit der Mittelwertberechnung kann bei entsprechend zur
Verfügung stehender Zeit (über den Kernlehrplan hinausgehend)
noch eine weitere wichtige Grundvorstellung des Integrals
erarbeitet werden.
|
Angestrebter Kompetenzerwerb
- Fettdruck: Vom Kernlehrplan verpflichtend vorgegebene
Kompetenzerwartungen.
- Fettdruck und Kursivdruck: Vom Kernlehrplan verpflichtend
vorgegebene Kompetenzerwartungen, die über das Grundkursniveau
hinausgehen.
- Normaldruck: Schulspezifische Kompetenzerwartungen.
Handlungsfeld „Integralrechnung“
- Ich kann an geeigneten
Beispielen den Übergang von der Produktsumme zum Integral
auf der Grundlage eines propädeutischen Grenzwertbegriffs
erläutern und vollziehen.
- Ich kann folgende Zusammenhänge richtig erläutern und in
Sachzusammenhängen anwenden:
- Ich kenne folgende Schritte zur näherungsweisen
Berechnung des Inhalts A der Fläche zwischen dem Graphen
von f und der x-Achse und den Begriff "Produktsumme":
- Gegeben ist die stetige Funktion f mit f(x) ≥ 0 für
x ∈ [a ; b]. Zur näherungsweisen Berechnung des
Inhaltes A der Fläche zwischen dem Grapgen von f und
der x-Achse über dem Intervall [a ; b] kann man so
vorgehen:
- Man wählt eine feste Zahl n und unterteilt das
Intervall [a ; b] in n gleichlange
Teilintervalle der Breite h = (b–a)/n.
- Aus jedem Teilintervall wählt man eine Stelle xi
für i = 1, 2, 3, ... , n und berechnet den
zugehörigen Funktionswert f(xi).
- Man berechnet als Näherungswert für den
Flächeninhalt die „Produktumme“
Sn = h · f(x1) + h · f(x2)
+ ... + h · f(xn) = h · [f(x1)
+ f(x2) + ... + f(xn)].
- Ich kenne die besonderen Produktsummen "Untersumme" und
"Obersumme", mit denen A "nach unten" bzw "nach oben"
abgeschätz wird. Bei der Untersumme wählt man für die Höhe
jedes Rechtecks den kleinsten Funktionswert des
entsprechenden Teilintervalls, bei der Obersumme den
größten.
- Ich kann folgende Definition des Integrals einer
Funktion f richtig angeben und erläutern:
- Die Funktion f sei auf dem Intervall [a ; b] stetig
und Sn eine beliebige Produktsumme mit Sn
= h·f(x1) + h·f(x2) + ... +
h·f(xn) und h = (b–a)/n. Dann heißt
der Grenzwert
 das Integral der Funktion f zwischen den
Grenzen a und b. Man schreibt dafür:
das Integral der Funktion f zwischen den
Grenzen a und b. Man schreibt dafür: 
- Ich kann folgende mathematische Bezeichnungen im
Zusammenhang mit dem Integral richtig benennen:
- Die Integralschreibweise wurde von Gottfried
Wilhelm Leibniz (1646 bis 1716) eingeführt.
- Das Integralzeichen ist aus einem S (von Summa)
entstanden.
- dx steht für immer kleiner werdende
Intervallbreiten h.
- Im Integralausdruck wird für
- f(x) die Bezeichnung Integrand und
für
- x die Bezeichnung Integrationsvariable
verwendet.
- Die Grenzen a und b heißen untere und obere
Integrationsgrenze.
- Ich kann den
Zusammenhang zwischen Änderungsrate und Integralfunktion
erläutern.
- Ich kann folgende Definition der Integralfunktion
richtig angeben und erläutern:
- Die Funktion f: t → f(t) sei in einem Intervall I
stetig und a ∈ I. Dann heißt die Funktion Ja
mit
 für x ∈ I Integralfunktion
(Flächeninhaltsfunktion) von f zur unteren
Grenze a.
für x ∈ I Integralfunktion
(Flächeninhaltsfunktion) von f zur unteren
Grenze a.
- Ich kann folgende Definition einer Stammfunktion richtig
angeben und erläutern:
- Eine Funktion F heißt Stammfunktion zu einer
Funktion f auf einem Intervall I, wenn für alle x ∈ I
gilt: F´(x) = f(x).
- Ich kann folgenden mathematischen Satz über
Stammfunktionen richtig angeben und erläutern:
- Ist F eine Stammfunktion von f in I, so gilt für
alle weiteren Stammfunktionen G von f in I: G(x) =
F(x) + c , c ∈ I mit einer Konstanten c.
- Ich kann den Hauptsatz
der Differential- und Integralrechnung unter Verwendung
eines anschaulichen Stetigkeitsbegriffs begründen.
- Ich kann die zwei Teile des Hauptsatzes der
Differential- und Integralrechnung richtig angeben
und erläutern:
- Die Funktion f sei im Intervall [a ; b] stetig. Dann
gilt:
- Teil 1: Existenz von Stammfunktionen
- Die Integralfunktion
(Flächeninhaltsfunktion)
 ist eine Stammfunktion von f.
ist eine Stammfunktion von f.
- Sie ist für alle x aus (a;b)
differenzierbar, und es gilt:
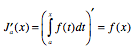
- Teil 2: Integralberechnung
- Mit einer beliebigen Stammfunktion F von f
kann das bestimmte Integral auf folgende Art
berechnet werden:
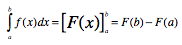
- Ich kann Stammfunktionen
ganzrationaler Funktionen bestimmen.
- Ich kann folgenden mathematischen Satz richtig angeben
und anwenden:
|
Funktion f |
Stammfunktion F von f
|
| Potenzfunktionen |
f(x) = xz |
F(x) = 1/(z+1)·xz+1 für z ∈ Z ohne {–1} |
Sind
U und V Stammfunktionen von u bzw. v, dann gilt:
|
|
f(x) = u(x) + v(x) |
F(x) = U(x) + V(x), |
|
f(x) = c · u(x) |
F(x) = c · U(x) |
| Lineare Verkettung |
f(x) = u(r·x+s) |
F(x) = 1/r · U(r·x+s) |
|
Aus f(x) = u(x) · v(x) folgt
nicht F(x) = U(x) · V(x). |
- Ich kann die natürliche
Logarithmusfunktion als Stammfunktion der Funktion x
→ 1/x nutzen.
- Ich kann die
Intervalladditivität und Linearität von Integralen nutzen.
- Ich kann folgenden mathematischen Satz richtig angeben
und anwenden:
- Sind die Funktionen f und g auf dem Intervall I
stetig und sind a , b, c ∈ I sowie r eine reelle Zahl,
so gilt:
- Intervalladditivität des Integral
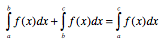
- Linearität des Integrals

- Ich kann den Gesamtbestand
oder Gesamteffekt einer Größe aus der Änderungsrate
ermittlen.
- Ich kann folgende zwei mathematische Sätze richtig
angeben und in Sachkontexten anwenden:
- Satz 1: Ist m(t) mit t ∈ [t1; t2]
die momentane Änderungsrate einer Größe G, dann erhält
man die Gesamtänderung G(t2)–G(t1)
der Größe im Intervall [t1; t2]
als Integral:
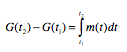
- Satz 2: Ist m(t) mit t ∈ [t1; t2]
die momentane Änderungsrate einer Größe G und G(t1)
der Bestand der Größe zum Zeitpunkt t1,
dann gilt für den Bestand der Größe zum Zeitpunkt t2:

- Ich kann Flächeninhalte
und Volumina von Körpern bestimmen, die durch die Rotation
um die Abszisse entstehen, mithilfe von bestimmten und
uneigentlichen Integralen.
- Ich kann folgende Schritte zur Flächenberechnung richtig
angeben und anwenden:
- Bei der Berechnung des Flächeninhalts zwischen dem
Graphen einer Funktion f und der x-Achse über dem
Intervall [a;b] geht man so vor:
- Man bestimmt die Nullstellen von f auf [a;b].
- Man untersucht, welches Vorzeichen f(x) in den
Teilintervallen hat.
- Man bestimmt die Inhalte der Teilflächen und
addiert sie.
- Wird eine Fläche über dem Intervall [a;b] von den
Graphen zweier Funktionen f und g begrenzt und gilt
f(x) ≥ g(x) für alle x ∈ [a;b], dann gilt für ihren
Inhalt A:
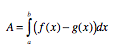
- Ich kann folgenden mathematischen Satz richtig angeben
und anwenden:
- Die Funktion f sei auf [a;b] stetig. Rotiert die
Fläche unter dem Graphen von f über dem Intervall
[a;b] um die x-Achse (Abszisse), so entsteht ein Rotationskörper.
Sein Volumen V beträgt
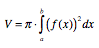
- Ich kann mithilfe des Integrals Mittelwerte von Funktionen
bestimmen.
- Ich kann die folgende Definition richtig benennen und
anwenden:
- Die Zahl
 heißt Mittelwert der Funktion f auf [a;b]
heißt Mittelwert der Funktion f auf [a;b]
Prozessbezogene Kompetenzen (Schwerpunke):
- Argumentieren
Die Schülerinnen und Schüler
- stellen Vermutungen auf (Vermuten)
- unterstützen Vermutungen beispielgebunden (Vermuten)
- präzisieren Vermutungen mithilfe von Fachbegriffen und
unter Berücksichtigung der logischen Struktur (Vermuten)
- stellen Zusammenhänge zwischen Begriffen her
(Begründen)
- Werkzeuge nutzen
Die Schülerinnen und Schüler
- Verwenden verschiedene digitale Werkzeuge zum
- Messen von Flächeninhalten zwischen Funktionsgraph
und Abszisse
- Ermitteln des Wertes eines bestimmten Integrals
|
 das Integral der Funktion f zwischen den
Grenzen a und b. Man schreibt dafür:
das Integral der Funktion f zwischen den
Grenzen a und b. Man schreibt dafür: 
 für x ∈ I Integralfunktion
(Flächeninhaltsfunktion) von f zur unteren
Grenze a.
für x ∈ I Integralfunktion
(Flächeninhaltsfunktion) von f zur unteren
Grenze a.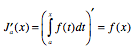
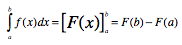
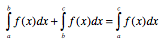

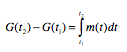

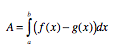
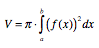
 heißt Mittelwert der Funktion f auf [a;b]
heißt Mittelwert der Funktion f auf [a;b]